Altitude (triangle)

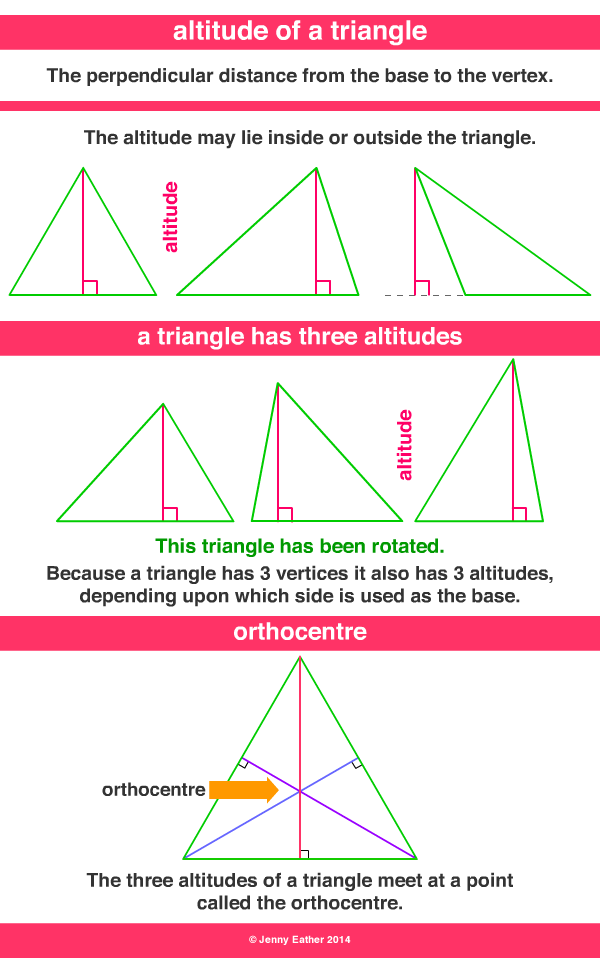
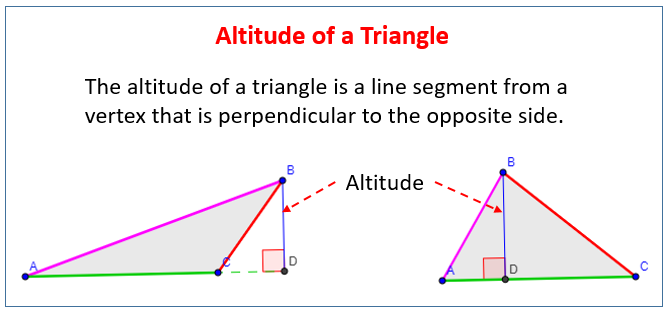
In geometry, an altitude of a triangle is a line segment through a given vertex (called apex) and perpendicular to a line containing the side or edge opposite the apex. This (finite) edge and (infinite) line extension are called, respectively, the base and extended base of the altitude. The point at the intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude" or "height", symbol h, is the distance between the foot and the apex. The process of drawing the altitude from a vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

Altitudes can be used in the computation of the area of a triangle: one-half of the product of an altitude's length and its base's length (symbol b) equals the triangle's area: A=hb/2. Thus, the longest altitude is perpendicular to the shortest side of the triangle. The altitudes are also related to the sides of the triangle through the trigonometric functions.

In an isosceles triangle (a triangle with two congruent sides), the altitude having the incongruent side as its base will have the midpoint of that side as its foot. Also the altitude having the incongruent side as its base will be the angle bisector of the vertex angle.

In a right triangle, the altitude drawn to the hypotenuse c divides the hypotenuse into two segments of lengths p and q. If we denote the length of the altitude by h_c, we then have the relation

${\displaystyle h_{c}={\sqrt {pq}}}$  (Geometric mean theorem; see Special Cases, inverse Pythagorean theorem)

For acute triangles, the feet of the altitudes all fall on the triangle's sides (not extended). In an obtuse triangle (one with an obtuse angle), the foot of the altitude to the obtuse-angled vertex falls in the interior of the opposite side, but the feet of the altitudes to the acute-angled vertices fall on the opposite extended side, exterior to the triangle. This is illustrated in the adjacent diagram: in this obtuse triangle, an altitude dropped perpendicularly from the top vertex, which has an acute angle, intersects the extended horizontal side outside the triangle.

Theorems

Orthocenter

Altitude in terms of the sides

For any triangle with sides a, b, c and semiperimeter ${\displaystyle s={\tfrac {1}{2}}(a b c),}$ the altitude from side a (the base) is given by

${\displaystyle h_{a}={\frac {2{\sqrt {s(s-a)(s-b)(s-c)}}}{a}}.}$

This follows from combining Heron's formula for the area of a triangle in terms of the sides with the area formula ${\displaystyle {\tfrac {1}{2}}\times {\text{base}}\times {\text{height}},}$ where the base is taken as side a and the height is the altitude from the vertex A (opposite side a).

By exchanging a with b or c, this equation can also used to find the altitudes h_b and h_c, respectively.

Inradius theorems

Consider an arbitrary triangle with sides a, b, c and with corresponding altitudes h_a, h_b, h_c. The altitudes and the incircle radius r are related by^{: Lemma 1}

${\displaystyle \displaystyle {\frac {1}{r}}={\frac {1}{h_{a}}} {\frac {1}{h_{b}}} {\frac {1}{h_{c}}}.}$

Circumradius theorem

Denoting the altitude from one side of a triangle as h_a, the other two sides as b and c, and the triangle's circumradius (radius of the triangle's circumscribed circle) as R, the altitude is given by

${\displaystyle h_{a}={\frac {bc}{2R}}.}$

Interior point

If p₁, p₂, p₃ are the perpendicular distances from any point P to the sides, and h₁, h₂, h₃ are the altitudes to the respective sides, then

${\displaystyle {\frac {p_{1}}{h_{1}}} {\frac {p_{2}}{h_{2}}} {\frac {p_{3}}{h_{3}}}=1.}$

Area theorem

Denoting the altitudes of any triangle from sides a, b, c respectively as h_a, h_b, h_c, and denoting the semi-sum of the reciprocals of the altitudes as ${\displaystyle H={\tfrac {h_{a}^{-1} h_{b}^{-1} h_{c}^{-1}}{2}}}$ we have

${\displaystyle \mathrm {Area} ^{-1}=4{\sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}.}$

General point on an altitude

If E is any point on an altitude AD of any triangle △ABC, then^: 77–78

${\displaystyle {\overline {AC}}^{2} {\overline {EB}}^{2}={\overline {AB}}^{2} {\overline {CE}}^{2}.}$

Triangle inequality

Since the area of the triangle is ${\displaystyle {\tfrac {1}{2}}ah_{a}={\tfrac {1}{2}}bh_{b}={\tfrac {1}{2}}ch_{c}}$, the triangle inequality ${\displaystyle a$ implies

${\displaystyle {\frac {1}{h_{a}}}<{\frac {1}{h_{b}}} {\frac {1}{h_{c}}}}$.

Special cases

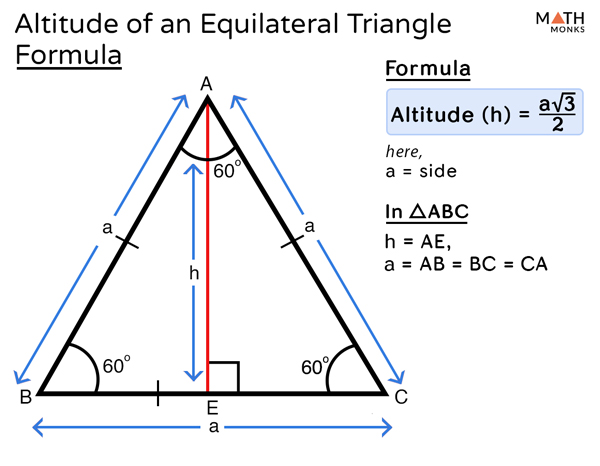
Equilateral triangle

From any point P within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. This is Viviani's theorem.

Right triangle

In a right triangle with legs a and b and hypotenuse c, each of the legs is also an altitude: ⁠${\displaystyle h_{a}=b}$⁠ and ⁠${\displaystyle h_{b}=a}$⁠. The third altitude can be found by the relation

${\displaystyle {\frac {1}{h_{c}^{2}}}={\frac {1}{h_{a}^{2}}} {\frac {1}{h_{b}^{2}}}={\frac {1}{a^{2}}} {\frac {1}{b^{2}}}.}$

This is also known as the inverse Pythagorean theorem.

Note in particular:

${\displaystyle {\begin{aligned}{\tfrac {1}{2}}AC\cdot BC&={\tfrac {1}{2}}AB\cdot CD\\[4pt]CD&={\tfrac {AC\cdot BC}{AB}}\\[4pt]\end{aligned}}}$

See also

• Median (geometry)

Notes

References

• Altshiller-Court, Nathan (2007) [1952], College Geometry, Dover
• Berele, Allan; Goldman, Jerry (2001), Geometry: Theorems and Constructions, Prentice Hall, ISBN 0-13-087121-4
• Bogomolny, Alexander. "Existence of the Orthocenter". Cut the Knot. Retrieved 2022-12-17.
• Johnson, Roger A. (2007) [1960], Advanced Euclidean Geometry, Dover, ISBN 978-0-486-46237-0
• Smart, James R. (1998), Modern Geometries (5th ed.), Brooks/Cole, ISBN 0-534-35188-3

External links

• Weisstein, Eric W. "Altitude". MathWorld.